フラクタル状に分岐しつつマンデルブロ海岸をなぞる非線形解説
ここではこのアプリの背景にある数学について簡単な説明をします。 ただ綺麗なだけでも十分に思われるかもしれませんが、仕組みも分かるともっと面白いし、 自分なりの工夫をして、新しいアプリを作ることもできます。
それにこのアプリに使ってる数学は単純なものなので、せいぜい高校で習うものだけで充分です。 具体的には、複素平面,数列,極限、程度です。 多少進んだ話題も取り上げますが、単なるおまけです。
このアプリの主な機能はジュリア集合を表示し、マウスや指の動きに合わせて変形していくことです。 そのためにまずジュリア集合について説明しましょう。
ジュリア集合は漸化式[1]zn+1=zn2+c (cは定数)を いろいろな複素数[2]の初期値(つまりz1の値)からスタートさせたときの挙動に関わる集合です。 いきなりcと初期値という、二つの動く数が出てきました。この時点で数学が苦手な人は混乱してしまいますね。 なので、まずcを固定します。特に簡単な場合を考えたいのでc=0としましょう。 すると漸化式はzn+1 = zn2となります。 つまり単に2乗していくだけです。 この数列をいろいろな初期値でシミュレーションしてみましょう。
まずアプリのページを開いて画像が白い円になっている状態で、画像の上にある「ジュリアを止める」というボタンを押してください。 すると画像が動かなくなります。 そして画像の中をクリックかタッチしてみてください。 すると、点が動いていくのが分かるでしょうか。 これがその点を初期値=スタート地点として、次の点を漸化式で計算していった数列の変化の仕方です。
白い円の外からスタートすると、画面の外に逃げていき、二度と帰ってきません。 これを発散といいます。 この画像ではさっさと発散してしまうスタート地点は黒く塗られています。
円の中からスタートすると、今度は円の中心に吸い込まれていくのが分かるでしょう。 この画像では発散しない点は白く塗られています。
この漸化式は単に2乗していくだけなので、絶対値を2乗、角度を2倍にしていくことになります。 なので、発散するかしないかを判定するのは難しくありません。
スタート地点の絶対値が1より大きければ、つまり円の外ならば、どんどん絶対値が大きくなり、画面の外へ逃げていき二度と帰ってきません。すなわち発散します。 スタート地点ノ絶対値が1より小さケレバ、つまり円の中ならば、絶対値はどんどん小さくなり、中心にどこまでも近づいていきます。コンピュータ上では精度の限界があるので、途中で0になります。よってこれは発散しません。 絶対値が丁度1、つまり円周上からスタートすると、いつまでも円周上にあります。よってこれも発散しません。
このように、cが0ならば、発散するかしないかは非常に簡単にわかります。 しかし、cを0以外の点にすると、発散するかしないかは、驚くほど複雑で入り組んだ図形を描くのです。
この画像では、発散するけど時間がかかる場合、どれくらい時間がかかったかで色分けをしています。 「ジュリア集合を動かす」ボタンを押して画像の上でマウスか指を動かすと、現在示している複素平面上の点をcとして、新しい漸化式で計算したジュリア集合が表示されます。
-
 c=iのとき
c=iのとき
デンドライト・フラクタル[3]
-
 c=-0.123+0.745i
c=-0.123+0.745i
ドゥアディの兎フラクタル[4]
-
 c=-0.75
c=-0.75
サンマルコ・フラクタル
-
 c=-0.391-0.587i
c=-0.391-0.587i
ジーゲル円盤フラクタル
表示には時間がかかるので、ゆっくり動かしてください。 ぜひ気に入った画像で「ジュリアを止める」ボタンを押すか、 画像をクリックするかして画像を止めて、動く点の様子を観察してください。 模様に沿った予想通りの動きをすることもあれば、 予想外の動きをすることもあって、面白いですよ。
様々なジュリア集合を観察すると、こんな簡単なルールから驚くほど複雑な図形が作られることに驚くのではないでしょうか。
ジュリア集合を見ると、 その小さな部分が大きな部分の繰り返しになっていることに気付きます。 こういう構造をフラクタルと言います。
フラクタルは、単純なルールから複雑な図形を作り出すのによく使われ、 最近だと映画『Dr. ストレンジ』が、 フラクタルを使って眩暈を起こすような映像をCGで作り上げていました。 また、枝が木の相似になり、 葉脈が枝の相似になり、 と自然界の一見複雑な図形も、 フラクタルと考えると、実は単純なやり方で実現されていることも多いです。
さて、ジュリア集合は 数列が発散するかどうかでそのスタート地点を分類したものです。 すると、次のこのジュリア集合を分類しようと思うのが数学では定石です。
cを決めるとジュリア集合が決まるので、これはcを分類すればいいでしょう。 その分類したものも、複素平面上の図形になります。
このこのように図形を分類したものをまた図形と考えたものを数学ではモジュライと読んだりします。
今考えてみるのは、ジュリア集合が白い部分を持ってるかどうかです。 特に注目するのは、画像の中心、つまり0をスタート地点としたとき、発散するかどうかです。
いろいろと画像を動かしてみて、中心が白くなっているcの集まりの輪郭が分かるでしょうか。 少し動かしただけで、画像が大きく変化してしまって、難しいのではないかと思います。
実際この境界はかなり複雑なのです。
もしここから境界がフラクタルになっている兆しが感じられたら非常に勘が鋭いと言えます。
では、「マンデルブロを表示」ボタンを押してみましょう。
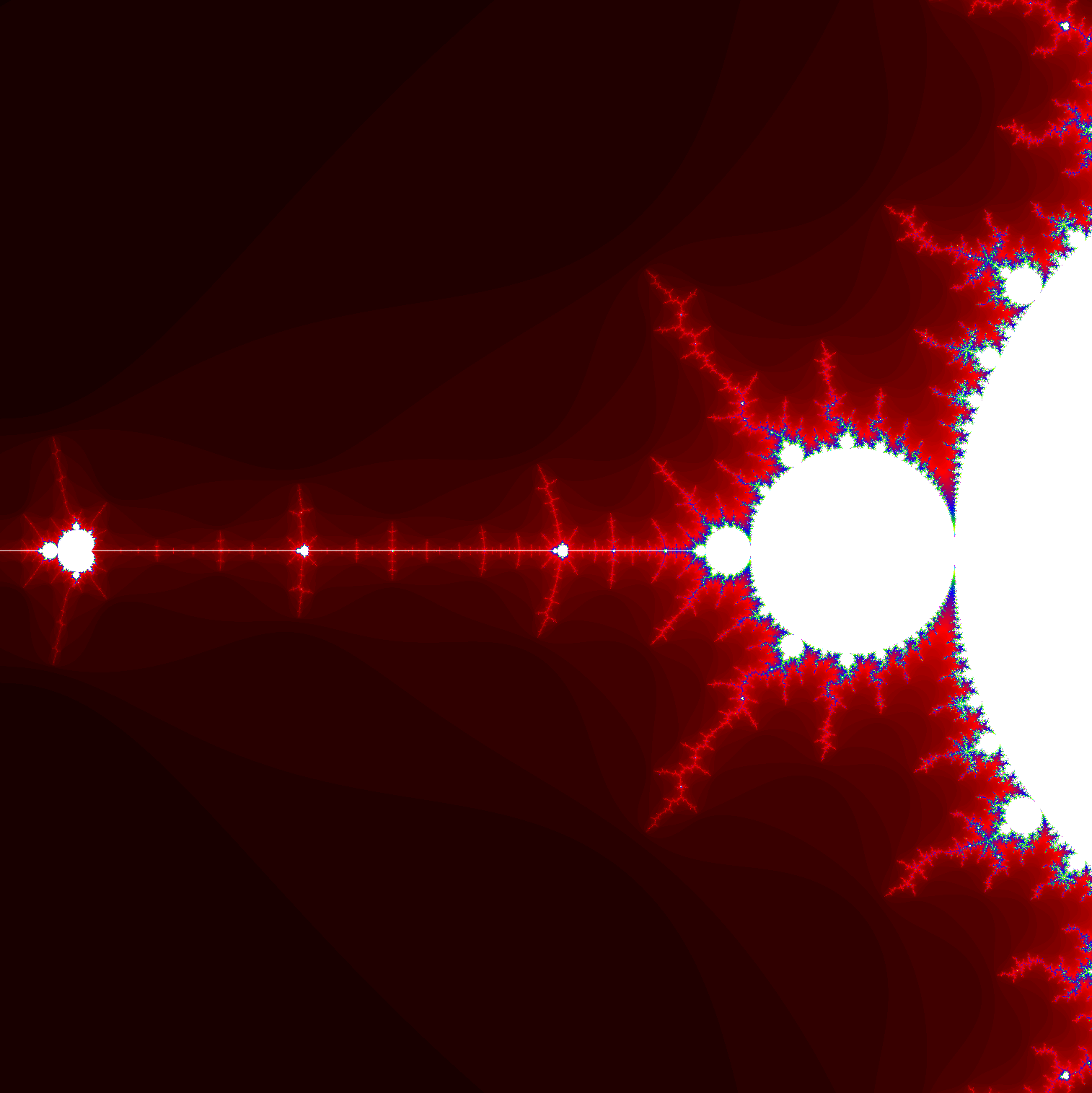
出てきた白い図形が、マンデルブロ集合、中心が白くなっているジュリア集合の集まりです。
その境界をなぞると、複雑怪奇なジュリア集合がたくさん現れることが分かります。 そしてこのマンデルブロ集合も、円形から円形が生えてそこからまた円形が生えて、と非常に複雑なフラクタルになっていることが分かりますね。
マンデルブロー集合

また細い道が何本も生えて外側に広がっているのも分かるでしょうか。
そこにまた急に白い部分が現れたりしていますね。そこも触って確かめてみましょう。
マンデルブロ集合が考えられ始めたときは、この「飛び地」のようなものが本当に飛び地なのかそれともつながっているのか謎でしたが、今は全てつながっていることが分かっています。
今回はそこまでの描写は行っていませんが、拡大すると、タツノオトシゴのような奇妙な構造が次々と現れます。興味を持ったらぜひweb上を調べていろいろな画像を見てください。
日本語版のwikiは貧弱ですが、英語版を見ればもう少しまともな情報にありつけますよ。英語が分かるならWolfram MathWorldというサイトが信頼性の高い情報を載せています。
[1] 数列とは単に数が順に並んでいるだけのものです。
例えば、1から始まって数が2倍になっていく等比数列は
1,2,4,8,...
であり、n番目の数をanと書くことにすると、この数列はan=2n-1と書けます。
このようにanをnの式で表したものを一般項といいます。
一般項が分かると、100番目の数だろうが1万番目の数だろうが、nにその数を代入すれば(一般項が計算できる式なら)計算できます。
これはどんな未来も分かることに対応しています。
そして、覚えているかどうか心配ですが、高校で習う数列の話は結局この一般項を求める話でしたね。
しかし、実際には一般的に数列の一般項を計算することは出来ません。
数列に限らず、一般的に一般的なものは一般的には手に入らないものなのです。
日常生活ではずっと未来のことは分からなくても、明日や一週間後などであればだいたい分かることも多いです。 たとえば作者はこれを作り始めたのち無職になりましたが、完成時には作り始めた時とは全く違う職種に復職していました。そんなこと全く予想できませんでしたよ。 そんな作者でも明日の予定くらいは、考えれば分かります。大概考えていないから、すっかり予定を忘れて大変なことになりますが (仮にダブルブッカー賞という賞があったらもらえるかもしれません。 クッツェーとかピーター・ケアリーとかがもらえる奴ではないと思います)。
というわけで、今日やっていることから明日やることを決めるその日暮らし的行動パターンに対応するのが漸化式です。
これはanをam(m < n)とnの式で表すものです。
高校の数学では漸化式から一般項を計算することをしましたね。覚えていないかもしれませんが。
これは言わば、明日のことしか分からない人が、ずっと先のことまで見通せるようになることに対応しています。
そんなことが出来たらいいですね。 だから高校の数学ではひたすら一般項を求めているわけですが、そもそも論に戻ると、 そんな夢みたいなこと本当にできるのでしょうか?
実は出来ません。
実は高校で習う漸化式に一般項が求められるのは、それが線形[5] もしくはほとんど線形なものばかりだからです。
線形な漸化式は割合簡単に解けますし、逆に言うと簡単に解ける漸化式とは、 線形な漸化式に変形できるものだ、とも言えます。
ところが世の中の大半のものは非線形なので、そんなに簡単に解けません。 でも科学者は諦めずに、そこから何かが分からないかと努力しています。
どうしても勉強はまず「解き方が分かっているもの」から始めるしかありませんが、 その先には「解き方が分かっていないけど、そこからどうにか断片的な知識でも導き出さなくちゃいけないもの」 がたくさんあって、そこが大事なんだ、ということが分かるといいですね。
これは学問に限らず、他の仕事とかも大体はそうです。
[2] 虚数単位iとは2乗すると-1になる数である。 そしてa+biという形に書ける数を複素数ということくらいは覚えているであろうと思う。
これはもともとは方程式を解くために便宜上導入された数です。
二次方程式は、複素数上で考えれば、重解含めて必ず2個解がある。 またカルダノによる三次方程式の解の公式では、解が全て実数でも計算途中で複素数が出てくる。
19世紀にはガウスが方程式は複素数上に必ず解を持つという代数学の基本定理を証明しました(複素数、というかその前の実数が少しも代数的な代物ではないので、 実は代数学の基本定理は少しも代数的な定理ではないし、当然証明も解析だったり幾何だったりと、少しも代数的ではなかったりしますが)。
その時にも、複素数を使わない書き方をして発表したほど、複素数への疑念はなかなか人々の間から去っていませんでした。
それらの疑念を払しょくするための重要な概念にもまたガウスの名前が付いています。 複素平面またの名をガウス平面です。(ガウス以前にも実は発明者はいたのですが、やはり普及に力があったのはガウスでしょう)。
-1倍にすることは実数直線で回れ右することに対応すると考えてみてください。 すると、虚数iとは何かという問いは、二回行うと回れ右になるものはなんだ、という問いだと解釈できます。 つまり右向け右、もしくは左向け左です。
数学界には反時計回りを正の向きだと考える慣習があるので、左向け左をiと考えましょう。
すると複素数a+biをx座標をa、y座標をbとしたベクトルととらえるなら、iを掛けるということは、このベクトルを半時計周りに90度回転させることを意味します。 また2を掛けるということは、ベクトルの実数倍と同じように、ベクトルを2倍に拡大することを意味します。 そしてその他の複素数を掛けることも全て、実数倍と回転に対応するわけです。
こうして、複素数は全て平面上の点を意味すると解釈できるようになりました。
ガウス平面によって、我々はiの存在論について何も悩む必要はなくったわけです。
今考えると虚数よりもよほど実数と呼ばれるものの方が、定義することも構成することも難しいし、存在論的な地位もあやしいので、 こちらについてはギリシャ以降は特に悩んでいないことのほうが驚きです。
複素数を使うと二次元の拡大や回転を掛け算で表すことができるのでとても便利です。
これを三次元に拡張したい、ということを考えたのがハミルトンです。
複素数が2つの数の組からなるので、自然な流れとして最初彼は数の三つ組みに、足し算引き算掛け算割り算のルールを入れようとしました。 ところがどうしても割り算が上手く上手くいかなくて悩んでいたある日、数の四つ組になら割り算までの計算のルールを入れられると発見したのです(実はガウスが先に発見していたらしいですが)。
それが四元数です。
四元数とは、i2=j2=k2=ijk=-1の関係が成り立つのi,j,kの三つの虚数単位 を使って、a+bi+cj+dkと書ける数です。
ハミルトンはこの関係式を思いついた時に渡っていたブルーム橋に刻みつけたと言います。
ハミルトンはこれを使うと3次元の回転が掛け算を使って (掛け算そのままではありませんが)表せられることに気づきます。
ハミルトンは今までの幾何は空間を扱い、 今までの代数は空間を扱うと考えていました。 カントを変なふうに読んでしまったらしく、 説明を読んでも正直よくわかりません。
とにかくそこから「時間と空間を統合した四元数は最強」 みたいな悟りに至ってしまい、 全てを四元数で説明するプロジェクトを推進します。 なんとなく物理学における「四次元空間」とか 「ミンコフスキー空間」と似ていますが、直接的関係はありません。
何しろハミルトンはアイルランド数学界の偉い人だったので、 色々な人が巻き込まれました。
例えば「スカラー」「ベクトル」の考え方は、 四元数の物理学への応用の中から生まれました。 マクスウェルの電磁気学も最初は四元数の言葉を使って書かれています。
しかし、その後ベクトルの概念の整備とともに、四元数にこだわる流儀は古臭くなって、一時期忘れ去られてしまいました。
しかし、時代とともに、無用なこだわりを捨てた目で見直すと、
- 物理学に顔を出す特殊なリー群の素性。
- なぜ低次元における位相幾何学には、高次元には表れない現象が起こるのか。
- 数論における多元環の重要さ。
など色々な場面で四元数が表れることが分かってきました。 例えば、 「なぜ我々の空間は一見3次元、時間も含めると4次元に見えるのか?」 などの答えを 解くのに、四元数が必要になることもありえるかもしれません。
ハミルトンは本人が思ってもいないところで、世界の謎にアクセスしてしまったかもしれないのです。
ちなみに三次元の回転は順序を変えると結果が変わります。
首を使って下を向いてから、 上下を軸に左に首を90度回転させると顎を左肩に乗せる形になりますが、 まっすぐ前を向いたまま上下を軸に左に首を90度回転させてから、 体の前方、つまり視線から右側に首を傾けると、 左を向きながら首をかしげている形になって、結果が変わります。
これは四元数の掛け算において、 可換法則、すなわちab=baが必ずしも成り立たないことに対応します。
対して二次元の回転では30度回転させたあとに90度回転させても、 90度回転させたあとに30度回転させても、結果は120度回転で変わりませんね。
これは複素数の掛け算において可換法則が成り立つことと対応しています。
四元数は空間の回転を簡単に表現できるので、 人工衛星の姿勢制御や、 3DCGの回転などに使われています。
可愛いキャラクターを音楽に合わせて踊らせられるソフトMikuMikuDanceでも、 関節の回転を四元数を使って表現しています。
対してMikuMikuDanceのカメラの回転は、 オイラー角という三次元回転の別の表現を使っています。 こちらのほうが少ない数字で表せられるのですが、 ジンバルロックという現象を起こす弱点を持つので、使い所が別なのです。
ぜひMikuMikuDanceで確かめてみてください。 可愛い、にも数学がいることがあるのです。
さらに世界を広げて行くと、どこまでも道が続いています。
四元数のもう一つ向こうには、八元数というものがあり、これは 結合法則(ab)c = a(bc)を満たしません。
計算が死ぬほど面倒になります。
こうしてこのような超複素数は、 十六元数三十二元数とどこまでも続いていきます。
私が作った任意の2n元数の計算ができるAndroid用の電卓アプリが 公開 されているので、興味を持った方は遊んでください。
[3] デンドライト とは複数に枝分かれした樹脂状結晶で、 自然現象で出来るフラクタルです。
過冷却状態や過飽和状態の 液体から固体が析出するときに、 飛び出た部分が成長しやすく、 ちょっとしたことで枝分かれしていくので起きます。 枝の角度は結晶の基本構造で決まっています。 例えば雪の結晶もデンドライトの一種です。
まるで植物のように見えるので、化石と間違われます。 こういうものを偽化石といいます。
逆に筆石と言うまるで文字のように見える化石は、 かつて偽化石と思われていました。
[4] アドリアン・ドゥアディはフランスの数学者。 ブルバキの一員。複素力学系の研究に大きな足跡を残し、 冬の地中海に飛び込んで死にました。
「フランスで英語の講演をするのは犯罪」というほどの「愛国語」主義者 [6]。 数学のワークショップ中に「フランス語で詩を読む会」を主催して、 皆でボードレールを朗読するほど。
フランスでは初等的な数学教育においても 「まずフランス語を学ぶことから始まる」 という雰囲気が強いとどこかでJacque Garigue氏も言っていた覚えがあります。
実際論文などもフランス語で書かれることがいまだにあるほどです。
[5] 線形であるとは、簡単に言えば比例のことで、 初期値、つまりa1の値を2倍すると、 それ以降の値は全て2倍になるし、 初期値を足し算すると、 それ以降の値も全て足し算になる、ということです。
数列で言えばこれはまさに 等比数列an+1=ranのことですね。
高校の数学で学ぶ数列の多くは、 結局は等比数列に治すことで解かれます。
同様に大学で習うものも、 多くは線形なもの、 あるいは線形なものに帰着できるものです。
実は線形でないもの、 つまり非線形なものを解くのは実はとても難しくなります。
なので非線形なものには分かっていないことが多く、 だからこそ学問としてはとても興味深いのです。
このアプリでも、 ものすごく簡単な非線形な式 zn+1=zn2+c について考えてみたわけですが、 こんな簡単な式からでも、 いくつもの予想不可能な挙動が引き出せました。
天気予報などが難しいことや、 フラクタルも含め自然界に様々なパターンが自然発生すること(自己組織化)、 生命現象や社会現象や経済現象などの複雑さの裏には、 この非線形性が潜んでいます。
科学では、 まず予想のしやすさから線形に見える現象から解析されていきました。 しかし、 だんだんと予想のしにくい非線形なものに 直面せざるを得なくなっています。
これは逆に言うと、 線形な科学の発展が、 とうとう非線形な世界にまで及ぼうとしているという風に見ることも可能です。
ちなみにこの解説自体も注釈の中に注釈が発生し(フラクタル)、 ひたすら分岐を繰り返しながら予測不可能に脱線[7]をしていく(カオス)、 非線形解説となっています。
非線形科学やフラクタル、複雑系、カオスなどは1990年代に、 一度ブームになりました。 その時期にそれらが通俗科学においてどう消費されていたかを知りたい人は、 作中のその名も「フラクタライズ・コンピュータ」なるものの暴走で物語が始まる 傑作群『恐竜惑星』『ジーンダイバー』に絡めて語っている この記事を参照してください。
[6] モデル理論という数理論理学の一分野の有名な学者 Bruno Poizatも「愛国語」主義者で、 論文集などを出しても一人だけフランス語で書いていたりすします。
モデル理論の有名な本を2冊出しましたが、 両方ともフランス語で、 お願いだが英語の翻訳をさせてくれ、 といろいろなところで言われていたらしいですけど、 なかなか首を縦に振りませんでした。
結局は両方とも英訳されたが、 その一冊『Stable Groups』の方は 「そこまでいうのなら」と自分で翻訳してしまいました。
この人スーパーマルチリンガルなので英訳くらい簡単にできるんですね。 その英訳版序文は「French. What a scientific language!」で始まり、 フランス語がどれくらい数学に適した言語であるかを とうとうと述べ立てています。
この神経、日本人も見習いたいですね。
ちなみに『Stable Groups』はもともと私家版をして出された本がもとで、 そちらのバージョンでは、 途中に水着の女性の写真が特に意味もなく挿入されていたらしいです。 そうしておけば生徒が読むかもしれない、ということらしいのですが、 今だと確実に性別差別で問題になりますね (数学を学ぶのは主に男性、 というステレオタイプがかつては世界中にあったことの証拠としては面白いかもしれません)。
索引に聞いたことのない女性の名前があるから当該ページを開いてみると、 写真モデルの女性の名前だったりするらしいです。 実物は坪井明人氏が持っているという話を聞いた覚えがあります。
Bruno Poizatの本にはいかにも言語マニアらしく、 ちょっとマニアックな文字で エピグラフ[9]が書いてあったりします。 『Stable Groups』の場合、 アラビア文字でした。 何が書いてあるんだろうと思っていたら、 あるときアルジェリア人と喋る機会があったので、 急いで本を持ってきて読んでもらった記憶があります。 「知識は最初は苦いが、だんだん甘くなる」というコーランの言葉だそうで、 なんだ、思ったより面白くないな、と正直思ってしまいました。
でもまあ、あまりエピグラフが面白すぎても、仕方がないですな。 例えば核物理学の教科書のエピグラフにデーヴァナーガリーで 「我は死なり。世界の破壊者なり」と書いてあったら、 面白いかもしれませんが、少しも適切ではありませんね。
[7] 脱線に関する話をすることで脱線してしまう、という手法を使った最初期の人物として、 『がリヴァー旅行記』の作者として知られる人間嫌いの天才風刺小説家ジョナサン・スウィフトが上げられます。
初期のブロニーでもあります。
[8] おや、真の孤立を探しにわざわざここまで来たのですか? それともよほど時代遅れの方ですか? まあどちらにしろよく来られた。何もないがゆっくりしていきなさい。
[9] エピグラフとは文書の巻頭に置かれる引用句のことで、 文書を要約したり、 他の作品と関連付けたりします。 要は雰囲気づくり。
学術書でしゃれたエピグラフと言えば、ミカエル・ニールセンとアイザック・チャンの共著『量子コンピュータと量子通信』の第4章の巻頭には
Daivid Deutschの
計算理論は従来純粋数学のテーマとして、ほとんどすべて抽象的思考で研究されてきた。これでは主要点を外すことになる。 コンピュータは物理的対象であり、計算は物理プロセスである。コンピュータが計算できるものできないものを決めるのは、物理法則のみであり、 純粋数学ではない。
という言葉と、ドナルド・クヌースの
コンピュータ科学は数学のように、他の科学とは何か異なったものになるであろう。そこでは正確に知ることのできない自然法則に代わって、証明できる人工的な法則が扱われる。
という言葉を並べて、最後にニールス・ボーアによる
深遠な真実の反対側にも、もう一つの深遠な真実があるかも知れない。
という相補性に関する言葉で締められます。 かっこいい。
学術書以外で好きなエピグラフですと、 ジョン・バースのエッセイ集『金曜日の本』のエピグラフが 『金曜日の本』のエピグラフ自身(つまり自分自身)から引用されている エピグラフに関する文章で若干のスベり笑いを誘いますが [10] 、フィクションで最高なのは、 ウンベルト・エーコの『フーコーの振り子』が、 レイモンド・スマリヤンの『紀元前5000年(邦題:哲学ファンタジー)』から
迷信は不幸を呼ぶ
を引いてくるものですね。
『フーコーの振り子』自体が迷信により呼び込まれた不幸のような話なので、 作品の要約になっているように感じられますが、 ここにはさらに裏の意味があります (ちなみに『フーコーの振り子』のテーマの一つは 「むやみに裏の意味を読むな」だったりしますけど)。
この文章はもともとの文脈では「自滅文」つまり、 「自分で自分を否定してしまう文」の例として出されているんですね。
例えば「時々雨が永遠に降り止まないことがある」とか 「許可駐車禁止」みたいな変な文です。
というのも、この文章は迷信を否定しているように見えて、 自分自身が迷信となってしまっている、というわけです。[11]
しかし、文脈を離れたエピグラフではそこまではなかなか読み取れませんね。
そして『フーコーの振り子』は、 「もともとの文脈から引き離されてしまった記号はいかようにも読める」 ということを、 テーマの一つにしているわけなです。 これぞ解釈のネットワーク!
ところで、もし文書の末尾に引用などを置くとしたら ハイポグラフ[12]っていうんですかね?
[10] そもそもこの本の正式な題が 『金曜日の本──あるいは、本の題名は直截的であるべきだし、副題は避けるべき』 という直裁的でなく副題付きの代物なので、 どんな本なのかは推して知るべし、という感じです。
ちなみに題名が直裁的でないことは本自身によって指摘されてます。
めんどくせえな。
[11] 迷信が不幸を呼ぶ科学的な理由は一切ないことはもちろんですが、 むしろ迷信が認識のコストを下げ、 かつては生存に有利に働いていた可能性は高かった、と考えることすら可能です。
今後人類にとって積極的に迷信を肯定することが 生存に有利になるとはあまり思えませんが、 迷信を撲滅しようとすることが生存に有利になることは 費用対効果を考えてもあり得そうにないと個人的には思ってます。
[12]
余はさまざまな未来──すべての未来にあらず──にたいし、余の八岐の園をゆだねる。
崔奔 『八岐の園』